ಬ್ಲ್ಯಾಕ್ ಸ್ಕೋಲ್ಸ್ ಮಾದರಿ ಎಂದರೇನು ಮತ್ತು ಅದನ್ನು ಹೇಗೆ ಲೆಕ್ಕ ಹಾಕುವುದು?

ಬ್ಲ್ಯಾಕ್-ಸ್ಕೋಲ್ಸ್-ಮರ್ಟನ್ (ಬಿಎಸ್ಎಂ (BSM)) ಮಾದರಿ ಎಂದೂ ಕರೆಯಲ್ಪಡುವ ಬ್ಲ್ಯಾಕ್-ಸ್ಕೋಲ್ಸ್ ಮಾದರಿಯು ಆಧುನಿಕ ಹಣಕಾಸಿನ ಸಿದ್ಧಾಂತದಲ್ಲಿ ಗಮನಾರ್ಹ ಪರಿಕಲ್ಪನೆಯಾಗಿದೆ. ಇದು ಸಮಯ ಮತ್ತು ಅಪಾಯವನ್ನು ಒಳಗೊಂಡಂತೆ ವಿವಿಧ ಅಂಶಗಳ ಆಧಾರದ ಮೇಲೆ ಆಯ್ಕೆಗಳ ಒಪ್ಪಂದಗಳಂತಹ ಡಿರೈವೇಟಿವ್‌ಗಳ ಸೈದ್ಧಾಂತಿಕ ಮೌಲ್ಯವನ್ನು ಅಂದಾಜು ಮಾಡುವ ಗಣಿತದ ಸಮೀಕರಣವಾಗಿದೆ. 1973 ರಲ್ಲಿ ಅಭಿವೃದ್ಧಿಪಡಿಸಲಾದ ಇದು, ಬೆಲೆ ಆಯ್ಕೆಗಳ ಒಪ್ಪಂದಗಳಿಗೆ ವ್ಯಾಪಕವಾಗಿ ಬಳಸಲಾದ ವಿಧಾನವಾಗಿದೆ.

ಬ್ಲ್ಯಾಕ್-ಸ್ಕೋಲ್ಸ್ ಮಾದರಿಯ ಇತಿಹಾಸ

ಬಿಎಸ್ಎಂ (BSM) ಮಾದರಿಯು 1973 ರಲ್ಲಿ ಅದನ್ನು ಪರಿಚಯಿಸಿದ ಫಿಶ್ಚರ್ ಬ್ಲ್ಯಾಕ್, ರಾಬರ್ಟ್ ಮರ್ಟನ್ ಮತ್ತು ಮೈರಾನ್ ಸ್ಕೋಲ್ಸ್‌ನ ಪರಿಕಲ್ಪನೆ ಆಗಿತ್ತು. ಪ್ರಸ್ತುತ ಸ್ಟಾಕ್ ಬೆಲೆಗಳು, ನಿರೀಕ್ಷಿತ ಡಿವಿಡೆಂಡ್‌ಗಳು, ಆಯ್ಕೆಯ ಸ್ಟ್ರೈಕ್ ಬೆಲೆ, ನಿರೀಕ್ಷಿತ ಬಡ್ಡಿ ದರಗಳು, ಗಡುವು ಮುಗಿಯುವ ಸಮಯ ಮತ್ತು ನಿರೀಕ್ಷಿತ ಅಸ್ಥಿರತೆಯಂತಹ ವೇರಿಯೇಬಲ್‌ಗಳನ್ನು ಬಳಸಿಕೊಂಡು ಒಪ್ಪಂದದ ಸೈದ್ಧಾಂತಿಕ ಮೌಲ್ಯವನ್ನು ನಿರ್ಧರಿಸುವ ಮೊದಲ ಗಣಿತ ವಿಧಾನವಾಗಿದೆ. ಈ ಮಾದರಿಯನ್ನು ಬ್ಲ್ಯಾಕ್ ಮತ್ತು ಸ್ಕೋಲ್ಸ್‌ 1973 ಪೇಪರ್‌ನಲ್ಲಿ ಪರಿಚಯಿಸಿದರು ಮತ್ತು ನಂತರ ಮೆರ್ಟನ್ ಅದನ್ನು ವಿಸ್ತರಿಸಿದರು. 1997 ರಲ್ಲಿ, ಸ್ಕೋಲ್ಸ್ ಮತ್ತು ಮೆರ್ಟನ್ ಅವರಿಗೆ ಆರ್ಥಿಕ ವಿಜ್ಞಾನದಲ್ಲಿ ನೊಬೆಲ್ ಸ್ಮಾರಕ ಪ್ರಶಸ್ತಿಯನ್ನು ನೀಡಲಾಯಿತು.

ಬ್ಲ್ಯಾಕ್-ಸ್ಕೋಲ್ಸ್ ಮಾದರಿ ಹೇಗೆ ಕೆಲಸ ಮಾಡುತ್ತದೆ

ಸ್ಟಾಕ್‌ಗಳು ಅಥವಾ ಫ್ಯೂಚರ್ಸ್ ಕಾಂಟ್ರಾಕ್ಟ್‌ಗಳಂತಹ ಹಣಕಾಸಿನ ಸಾಧನಗಳು, ನಿರಂತರ ಡ್ರಿಫ್ಟ್ ಮತ್ತು ಅಸ್ಥಿರತೆಯೊಂದಿಗೆ ಯಾದೃಚ್ಛಿಕ ನಡೆಯನ್ನು ಅನುಸರಿಸಿ, ಬೆಲೆಗಳ ಸಾಮಾನ್ಯ ವಿತರಣೆಯನ್ನು ಪ್ರದರ್ಶಿಸುತ್ತವೆ ಎಂದು ಬಿಎಸ್ಎಂ (BSM) ಮಾಡೆಲ್ ಊಹಿಸುತ್ತದೆ. ಮಾಡೆಲ್‌ಗೆ ಐದು ವೇರಿಯೇಬಲ್‌ಗಳ ಅಗತ್ಯವಿದೆ: ಅಸ್ಥಿರತೆ, ಆಧಾರವಾಗಿರುವ ಆಸ್ತಿಯ ಬೆಲೆ, ಆಯ್ಕೆಯ ಸ್ಟ್ರೈಕ್ ಬೆಲೆ, ಆಯ್ಕೆಯ ಗಡುವು ಮುಗಿಯುವವರೆಗೆ ಸಮಯ ಮತ್ತು ಅಪಾಯ-ಮುಕ್ತ ಬಡ್ಡಿ ದರ. ಈ ವೇರಿಯೇಬಲ್‌ಗಳೊಂದಿಗೆ, ಮಾಡೆಲ್ ಯುರೋಪಿಯನ್-ಸ್ಟೈಲ್ ಕರೆ ಆಯ್ಕೆಯ ಬೆಲೆಯನ್ನು ಲೆಕ್ಕ ಹಾಕುತ್ತದೆ.

ಬ್ಲ್ಯಾಕ್-ಸ್ಕೋಲ್ಸ್ ಊಹೆಗಳು

ಬ್ಲ್ಯಾಕ್-ಸ್ಕೋಲ್ಸ್ ಮಾದರಿಯು ಹಲವಾರು ಊಹೆಗಳನ್ನು ನೀಡುತ್ತದೆ:

• ಆಯ್ಕೆಯ ಉದ್ದಕ್ಕೂ ಯಾವುದೇ ಡಿವಿಡೆಂಡ್‌ಗಳನ್ನು ಪಾವತಿಸಲಾಗುವುದಿಲ್ಲ.
• ಮಾರುಕಟ್ಟೆಗಳು ಯಾದೃಚ್ಛಿಕವಾಗಿವೆ, ಅಂದರೆ ಮಾರುಕಟ್ಟೆ ಚಲನೆಗಳನ್ನು ಅಂದಾಜು ಮಾಡಲಾಗುವುದಿಲ್ಲ.
• ಆಯ್ಕೆಯನ್ನು ಖರೀದಿಸುವಲ್ಲಿ ಯಾವುದೇ ಟ್ರಾನ್ಸಾಕ್ಷನ್ ವೆಚ್ಚಗಳಿಲ್ಲ.
• ಅಪಾಯ-ರಹಿತ ದರ ಮತ್ತು ಆಧಾರವಾಗಿರುವ ಆಸ್ತಿಯ ಅಸ್ಥಿರತೆಯನ್ನು ತಿಳಿದುಕೊಳ್ಳಲಾಗುತ್ತದೆ ಮತ್ತು ಸ್ಥಿರವಾಗಿರುತ್ತದೆ.
• ಆಧಾರವಾಗಿರುವ ಆಸ್ತಿಯ ಆದಾಯವನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ವಿತರಿಸಲಾಗುತ್ತದೆ.
• ಈ ಆಯ್ಕೆಯು ಯುರೋಪಿಯನ್ ಆಗಿದೆ ಮತ್ತು ಅವಧಿ ಮುಗಿಯುವ ಸಮಯದಲ್ಲಿ ಮಾತ್ರ ಅದನ್ನು ಬಳಸಬಹುದು.

ಬ್ಲ್ಯಾಕ್ ಸ್ಕಾಲ್ಸ್ ಮಾಡೆಲ್ ಫಾರ್ಮುಲಾ

ಸಂಚಿತ ಮಾನಕ ಸಾಮಾನ್ಯ ಸಂಭಾವ್ಯತೆ ವಿತರಣೆ ಕಾರ್ಯನಿರ್ವಹಣೆಯಿಂದ ಸ್ಟಾಕ್ ಬೆಲೆಯನ್ನು ಗುಣಿಸುವ ಮೂಲಕ ಬ್ಲ್ಯಾಕ್ ಸ್ಕೋಲ್ಸ್ ಫಾರ್ಮುಲಾವನ್ನು ಲೆಕ್ಕ ಹಾಕಲಾಗುತ್ತದೆ. ನಂತರ, ಸಂಚಿತ ಮಾನದಂಡದ ಸಾಮಾನ್ಯ ವಿತರಣೆಯಿಂದ ಗುಣಿಸಲಾದ ಸ್ಟ್ರೈಕ್ ಬೆಲೆಯ ನೆಟ್ ಪ್ರೆಸೆಂಟ್ ವ್ಯಾಲ್ಯೂ ಎನ್ ಪಿ ವಿ (NPV) ಅನ್ನು ಹಿಂದಿನ ಲೆಕ್ಕಾಚಾರದ ಫಲಿತಾಂಶ ಮೌಲ್ಯದಿಂದ ಕಡಿತಗೊಳಿಸಲಾಗುತ್ತದೆ.

ಅದರ ಗಣಿತದ ನಿರೂಪಣೆ ಇಲ್ಲಿದೆ:

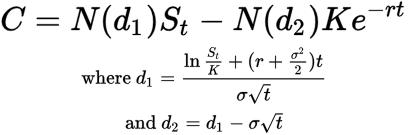
ಎಲ್ಲಿ,

C = ಕರೆ ಆಯ್ಕೆ ಬೆಲೆ

N = ಸಾಮಾನ್ಯ ವಿತರಣೆಯ ಸಿ ಡಿ ಎಫ್ (CDF)

St = ಆಸ್ತಿಯ ಸ್ಪಾಟ್ ಬೆಲೆ

K = ಸ್ಟ್ರೈಕ್ ಬೆಲೆ

R = ಅಪಾಯ-ರಹಿತ ಬಡ್ಡಿ ದರ

T = ಮೆಚ್ಯೂರಿಟಿಯ ಸಮಯ

P = ಆಸ್ತಿಯ ಅಸ್ಥಿರತೆ

ಬ್ಲ್ಯಾಕ್-ಸ್ಕೋಲ್ಸ್ ಮಾಡೆಲ್‌ನ ಪ್ರಯೋಜನಗಳು

1. ಇದು ಬೆಲೆ ಆಯ್ಕೆಗಳಿಗೆ ಸೈದ್ಧಾಂತಿಕ ಚೌಕಟ್ಟನ್ನು ಒದಗಿಸುತ್ತದೆ, ಆ ಮೂಲಕ ಹೂಡಿಕೆದಾರರು ಮತ್ತು ಟ್ರೇಡರ್ ಗಳಿಗೆ ರಚನಾತ್ಮಕ, ವ್ಯಾಖ್ಯಾನಿತ ವಿಧಾನವನ್ನು ಬಳಸಿಕೊಂಡು ಆಯ್ಕೆಯ ನ್ಯಾಯೋಚಿತ ಬೆಲೆಯನ್ನು ನಿರ್ಧರಿಸಲು ಅನುವು ಮಾಡಿಕೊಡುತ್ತದೆ.
2. ಇದು ಹೂಡಿಕೆದಾರರಿಗೆ ವಿವಿಧ ಸ್ವತ್ತುಗಳಿಗೆ ತಮ್ಮ ಅಪಾಯದ ಮಾನ್ಯತೆಯನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ಅನುವು ಮಾಡಿಕೊಡುವ ಮೂಲಕ ರಿಸ್ಕ್ ಮ್ಯಾನೇಜ್ಮೆಂಟನ್ನು ಸಕ್ರಿಯಗೊಳಿಸುತ್ತದೆ.
3. ವಿವಿಧ ಆಯ್ಕೆಗಳಿಗೆ ಸಂಬಂಧಿಸಿದ ನಿರೀಕ್ಷಿತ ಆದಾಯ ಮತ್ತು ಅಪಾಯಗಳ ಅಳತೆಯನ್ನು ಒದಗಿಸುವ ಮೂಲಕ ಪೋರ್ಟ್‌ಫೋಲಿಯೋ ಆಪ್ಟಿಮೈಸೇಶನ್‌ಗಾಗಿ ಇದನ್ನು ಬಳಸಬಹುದು.
4. ಟ್ರೇಡರ್ ಗಳು ಮತ್ತು ಹೂಡಿಕೆದಾರರು ಬೆಲೆ ಮತ್ತು ಟ್ರೇಡ್ ನ ಆಯ್ಕೆಗಳನ್ನು ಉತ್ತಮವಾಗಿ ಮಾಡಬಹುದಾದರಿಂದ ಇದು ಮಾರುಕಟ್ಟೆ ದಕ್ಷತೆ ಮತ್ತು ಪಾರದರ್ಶಕತೆಯನ್ನು ಹೆಚ್ಚಿಸುತ್ತದೆ.
5. ಇದು ಬೆಲೆಯನ್ನು ಸುಗಮಗೊಳಿಸುವ ಮೂಲಕ ವಿವಿಧ ಮಾರುಕಟ್ಟೆಗಳು ಮತ್ತು ಅಧಿಕಾರ ವ್ಯಾಪ್ತಿಗಳಲ್ಲಿ ಹೆಚ್ಚಿನ ಸ್ಥಿರತೆ ಮತ್ತು ಹೋಲಿಕೆಯನ್ನು ಅನುಮತಿಸುತ್ತದೆ.

ಹೂಡಿಕೆದಾರರಿಗೆ ಹೇಗೆ ಪ್ರಯೋಜನ ನೀಡಬಹುದು ಎಂಬುದರ ಕೆಲವು ನಿರ್ದಿಷ್ಟ ಉದಾಹರಣೆಗಳು ಇಲ್ಲಿವೆ:

• ಆಯ್ಕೆಯ ನ್ಯಾಯೋಚಿತ ಬೆಲೆಯನ್ನು ನಿರ್ಧರಿಸಲು. ಆಯ್ಕೆಯ ಸೈದ್ಧಾಂತಿಕ ಬೆಲೆಯನ್ನು ಲೆಕ್ಕ ಹಾಕಲು ಬ್ಲ್ಯಾಕ್-ಸ್ಕೋಲ್ಸ್ ಮಾದರಿಯನ್ನು ಬಳಸಬಹುದು, ಇದನ್ನು ನಂತರ ಮಾರುಕಟ್ಟೆ ಬೆಲೆಗೆ ಹೋಲಿಸಿದರೆ ಆಯ್ಕೆಯು ಕಡಿಮೆ ಮೌಲ್ಯಯುತವಾಗಿದೆಯೇ ಅಥವಾ ಹೆಚ್ಚು ಮೌಲ್ಯಯುತವಾಗಿದೆಯೇ ಎಂದು ನೋಡಬಹುದು.
• ಅಪಾಯದ ವಿರುದ್ಧ ರಕ್ಷಣೆ ನೀಡಲು. ಆಯ್ಕೆಯನ್ನು ಖರೀದಿಸುವ ಮೂಲಕ, ಹೂಡಿಕೆದಾರರು ಆಧಾರವಾಗಿರುವ ಆಸ್ತಿಯ ಬೆಲೆ ಕಡಿಮೆಯಾಗುವ ಅಪಾಯದ ವಿರುದ್ಧ ತಮ್ಮನ್ನು ತಾವು ರಕ್ಷಿಸಿಕೊಳ್ಳಬಹುದು. ಉದಾಹರಣೆಗೆ, ಒಂದು ಹೂಡಿಕೆದಾರರು ಕಂಪನಿಯಲ್ಲಿ ಷೇರುಗಳನ್ನು ಹೊಂದಿದ್ದರೆ, ಅವರು ಆ ಷೇರುಗಳಲ್ಲಿ ಒಂದು ನಿರ್ದಿಷ್ಟ ಮಟ್ಟಕ್ಕಿಂತ ಕಡಿಮೆ ಇರುವ ಷೇರು ಬೆಲೆಯ ಅಪಾಯದ ವಿರುದ್ಧ ತಮ್ಮನ್ನು ರಕ್ಷಿಸಲು ಆಯ್ಕೆಯನ್ನು ಖರೀದಿಸಬಹುದು.
• ಟ್ರೇಡಿಂಗ್ ಕಾರ್ಯತಂತ್ರಗಳನ್ನು ರಚಿಸಲು. ಇತರ ಹಣಕಾಸು ಸಾಧನಗಳೊಂದಿಗೆ ಆಯ್ಕೆಗಳನ್ನು ಸಂಯೋಜಿಸುವ ಮೂಲಕ, ಹೂಡಿಕೆದಾರರು ವಿವಿಧ ಮಾರುಕಟ್ಟೆ ಪರಿಸ್ಥಿತಿಗಳಲ್ಲಿ ಲಾಭಗಳನ್ನು ಸೃಷ್ಟಿಸಲು ಕಾರ್ಯತಂತ್ರಗಳನ್ನು ರಚಿಸಬಹುದು.

ಬ್ಲ್ಯಾಕ್-ಸ್ಕೋಲ್ಸ್ ಮಾದರಿಯ ಮಿತಿಗಳು

ಅದರ ಪ್ರಯೋಜನಗಳ ಹೊರತಾಗಿಯೂ, ಬ್ಲ್ಯಾಕ್-ಸ್ಕೋಲ್ಸ್ ಮಾದರಿಯು ಕೆಲವು ಮಿತಿಗಳನ್ನು ಹೊಂದಿದೆ:

1. ಇದನ್ನು ಯುರೋಪಿಯನ್ ಆಯ್ಕೆಗಳ ಬೆಲೆಗೆ ಮಾತ್ರ ಬಳಸಲಾಗುತ್ತದೆ ಮತ್ತು ಅಮೇರಿಕನ್ ಆಯ್ಕೆಗಳನ್ನು ಮುಕ್ತಾಯ ದಿನಾಂಕದ ಮೊದಲು ಚಲಾಯಿಸಬಹುದು ಎಂಬ ಅಂಶವನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳುವುದಿಲ್ಲ.
2. ಇದು ಡಿವಿಡೆಂಡ್‌ಗಳು ಮತ್ತು ಅಪಾಯ-ಮುಕ್ತ ದರಗಳು ಸ್ಥಿರವಾಗಿರುತ್ತವೆ ಎಂದು ಊಹಿಸುತ್ತದೆ, ಇದು ಯಾವಾಗಲೂ ಹಾಗಿರುವುದಿಲ್ಲ.
3. ಇದು ಅಸ್ಥಿರತೆಯು ಆಯ್ಕೆಯ ಜೀವನದ ಉದ್ದಕ್ಕೂ ಸ್ಥಿರವಾಗಿರುತ್ತದೆ ಎಂದು ಊಹಿಸುತ್ತದೆ, ಆದರೆ ಸಾಮಾನ್ಯವಾಗಿ ಅಸ್ಥಿರತೆಯು ಸರಬರಾಜು ಮತ್ತು ಬೇಡಿಕೆಯ ಮಟ್ಟದೊಂದಿಗೆ ಏರಿಳಿತವಾಗುವುದಿಲ್ಲ.
4. ಇದು ಯಾವುದೇ ಟ್ರಾನ್ಸಾಕ್ಷನ್ ವೆಚ್ಚಗಳು ಅಥವಾ ತೆರಿಗೆಗಳು ಇಲ್ಲದಿರುವುದು, ಎಲ್ಲಾ ಮೆಚ್ಯೂರಿಟಿಗಳಿಗೆ ನಿರಂತರ ಅಪಾಯ-ಮುಕ್ತ ಬಡ್ಡಿ ದರಗಳು ಮತ್ತು ಯಾವುದೇ ಅಪಾಯರಹಿತ ಮಧ್ಯಸ್ಥಿಕೆ ಅವಕಾಶಗಳಿಲ್ಲದಂತಹ ಹಲವಾರು ಇತರ ಅಂದಾಜುಗಳನ್ನು ಮಾಡುತ್ತದೆ. ಈ ಊಹೆಗಳು ನಿಜವಾದ ಫಲಿತಾಂಶಗಳಿಂದ ವಿಚಲನಗೊಳ್ಳುವ ಬೆಲೆಗಳಿಗೆ ಕಾರಣವಾಗಬಹುದು.
5. ಇದು “ಬ್ಲ್ಯಾಕ್ ಬಾಕ್ಸ್” ಮಾದರಿಯಾಗಿದೆ. ಇದರರ್ಥ ಮಾಡೆಲ್ ಅದರ ಫಲಿತಾಂಶಗಳನ್ನು ಹೇಗೆ ತಲುಪುತ್ತದೆ ಎಂಬುದು ಯಾವಾಗಲೂ ಸ್ಪಷ್ಟವಾಗಿಲ್ಲ. ಆಯ್ಕೆಯ ಬೆಲೆಗಳ ಮೇಲೆ ಪರಿಣಾಮ ಬೀರುವ ಆಧಾರವಾಗಿರುವ ಅಂಶಗಳನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ಮಾದರಿಯನ್ನು ಬಳಸಲು ಇದು ಕಷ್ಟಕರವಾಗಿಸುತ್ತದೆ.

FAQs