ब्लॅक-स्कॉल्स मॉडेल, ज्याला ब्लॅक-स्कॉल्स-मर्टन (बीएसएम) (BSM) मॉडेल म्हणूनही ओळखले जाते, आधुनिक वित्तीय सिद्धांतामध्ये महत्त्वपूर्ण संकल्पना आहे. हे एक गणितीय समीकरण आहे जे वेळ आणि जोखीम यासह विविध घटकांवर आधारित डेरिव्हेटिव्ह्जच्या सैद्धांतिक मूल्याचा अंदाज लावते, जसे की पर्याय करार. 1973 मध्ये विकसित केलेली, ही किंमत पर्याय करारासाठी मोठ्या प्रमाणावर वापरली जाणारी पद्धत आहे.
ब्लॅक-स्कॉल्स मॉडेलचा इतिहास
बीएसएम (BSM) मॉडेल हे फिशर ब्लॅक, रॉबर्ट मेर्टन आणि मायरॉन स्कोलेस यांच्या बुद्धीची उपज होती, ज्यांनी ते 1973 मध्ये सादर केले. सध्याच्या स्टॉकच्या किमती, अपेक्षित लाभांश, पर्यायाची स्ट्राइक किंमत, अपेक्षित व्याजदर, मुदत संपण्याची वेळ आणि अपेक्षित अस्थिरता यासारख्या व्हेरिएबल्सचा वापर करून ऑप्शन कॉन्ट्रॅक्टचे सैद्धांतिक मूल्य ठरवण्याचा हा पहिला गणिती दृष्टिकोन होता. हे मॉडेल 1973 च्या पेपरमध्ये ब्लॅक आणि स्कोल्सने सादर केले होते आणि नंतर मर्टनने त्याचा विस्तार केला होता. 1997 मध्ये, स्कोल्स आणि मेर्टन यांना त्यांच्या मॉडेलवरील कामासाठी अर्थशास्त्रातील नोबेल मेमोरियल पारितोषिक देण्यात आले.
ब्लॅक स्कॉल्स मॉडेल कसे काम करते
बीएसएम (BSM) मॉडेल असे गृहीत धरते की आर्थिक साधने, जसे की स्टॉक किंवा फ्युचर्स कॉन्ट्रॅक्ट्स, सतत वाहून जाणे आणि अस्थिरतेसह यादृच्छिक चालानंतर, किमतींचे असामान्य वितरण प्रदर्शित करतील. मॉडेलला पाच व्हेरिएबल्सची आवश्यकता आहे: अस्थिरता, अंतर्निहित मालमत्तेची किंमत, पर्यायाची स्ट्राइक किंमत, पर्यायाची मुदत संपेपर्यंत वेळ आणि जोखीम-मुक्त व्याज दर. या व्हेरिएबल्ससह, मॉडेल युरोपियन-शैलीतील कॉल पर्यायाची किंमत मोजते.
ब्लॅक-स्कॉल्स गृहितके
ब्लॅक-स्कोल्स मॉडेल अनेक गृहीतके बनवते:
- पर्यायाच्या जीवनकाळात कोणताही लाभांश दिला जात नाही.
- बाजार यादृच्छिक असतात, याचा अर्थ बाजाराच्या हालचालींचा अंदाज लावता येत नाही.
- ऑप्शन खरेदी करण्यासाठी कोणतेही ट्रान्झॅक्शन खर्च नाहीत.
- अंतर्निहित मालमत्तेचा जोखीम-मुक्त दर आणि अस्थिरता ज्ञात आणि स्थिर आहेत.
- अंतर्निहित मालमत्तेचे रिटर्न सामान्यपणे वितरित केले जातात.
- हा पर्याय युरोपियन आहे आणि केवळ कालबाह्य झाल्यावर वापरला जाऊ शकतो.
ब्लॅक स्कॉल्स मॉडेल फॉर्म्युला
ब्लॅक-स्कोल्स फॉर्म्युला संचयी मानक सामान्य संभाव्यता वितरण कार्याद्वारे स्टॉकच्या किमतीचा गुणाकार करून गणना केली जाते. त्यानंतर, स्ट्राइक किंमतीचे निव्वळ वर्तमान मूल्य (एनपीवी) (NPV) संचयी मानक सामान्य वितरणाने गुणाकार केले जाते आणि मागील गणनेच्या परिणामी मूल्यातून वजा केले जाते.
येथे त्याचे गणितीय सूत्र आहे:
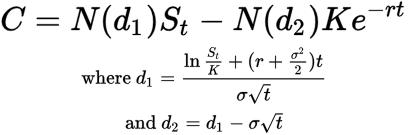
जिथे,
सी (C) = कॉल ऑप्शन किंमत
एन (N) = सामान्य वितरणाचे सीडीएफ (CDF)
एसटी (St) = ॲसेटची स्पॉट किंमत
के (K) = स्ट्राईक किंमत
आर (R) = रिस्क-फ्री इंटरेस्ट रेट
टी (T) = मॅच्युरिटीची वेळ
σ = मालमत्तेची अस्थिरता
ब्लॅक-स्कॉल्स मॉडेलचे लाभ
- हे किंमत पर्यायांसाठी एक सैद्धांतिक फ्रेमवर्क प्रदान करते, ज्यामुळे गुंतवणूकदार आणि व्यापार्यांना संरचित, परिभाषित पद्धती वापरून पर्यायाचे वाजवी मूल्य निर्धारित करता येते.
- हे गुंतवणूकदारांना वेगवेगळ्या मालमत्तेचे एक्सपोजर समजून घेण्यास अनुमती देऊन जोखीम व्यवस्थापन सक्षम करते.
- अपेक्षित परतावा आणि विविध पर्यायांशी संबंधित जोखीम यांचे मोजमाप देऊन पोर्टफोलिओ ऑप्टिमायझेशनसाठी याचा वापर केला जाऊ शकतो.
- यामुळे बाजाराची कार्यक्षमता आणि पारदर्शकता वाढते कारण व्यापारी आणि गुंतवणूकदार किंमत आणि व्यापार पर्याय अधिक चांगल्या प्रकारे सक्षम आहेत.
- हे विविध बाजारपेठा आणि अधिकारक्षेत्रांमध्ये अधिक सुसंगतता आणि तुलनात्मकता अनुमती देऊन किंमती सुव्यवस्थित करते.
ब्लॅक-स्कोल्स मॉडेलचा गुंतवणूकदारांना कसा फायदा होऊ शकतो याची काही विशिष्ट उदाहरणे येथे आहेत:
- ऑप्शनची योग्य किंमत निर्धारित करण्यासाठी. ब्लॅक-स्कोल्स मॉडेलचा वापर पर्यायाच्या सैद्धांतिक मूल्याची गणना करण्यासाठी केला जाऊ शकतो, ज्याची बाजारभावाशी तुलना केली जाऊ शकते हे पाहण्यासाठी पर्याय कमी किंवा जास्त मूल्यवान आहे.
- धोका टाळण्यासाठी. ऑप्शन खरेदी करून, गुंतवणूकदार अंतर्निहित मालमत्तेच्या किमतीत घट होण्याच्या जोखमीपासून स्वतःचे संरक्षण करू शकतो. उदाहरणार्थ, जर एखाद्या गुंतवणूकदाराकडे एखाद्या कंपनीचे शेअर्स असतील, तर ते शेअर्सची किंमत विशिष्ट पातळीच्या खाली येण्याच्या जोखमीपासून स्वतःचे संरक्षण करण्यासाठी त्या शेअर्सवर पुट ऑप्शन्स खरेदी करू शकतात.
- ट्रेडिंग धोरणे तयार करण्यासाठी. इतर आर्थिक साधनांसह पर्याय एकत्र करून, गुंतवणूकदार विविध बाजार परिस्थितींमध्ये नफा मिळविण्यासाठी धोरणे तयार करू शकतात.
ब्लॅक-स्कॉल्स मॉडेलच्या मर्यादा
त्याचे फायदे असूनही, ब्लॅक-स्कोल्स मॉडेलला काही मर्यादा आहेत:
- हे केवळ युरोपियन पर्यायांच्या किंमतीसाठी वापरले जाते आणि अमेरिकन ऑप्शन्सचा वापर कालबाह्य तारखेपूर्वी केला जाऊ शकतो हे लक्षात घेत नाही.
- हे असे गृहीत धरते की लाभांश आणि जोखीम मुक्त दर स्थिर आहेत, जे नेहमीच असू शकत नाहीत.
- हे असे गृहीत धरते की पर्यायाच्या आयुष्यभर अस्थिरता कायम राहते, जे पुरवठा आणि मागणीच्या पातळींसह अस्थिरता चढ-उतार होत असल्याने बहुतेकदा असे नसते.
- हे इतर अनेक गृहितक बनवते, जसे की कोणतेही व्यवहार खर्च किंवा कर नाही, सर्व परिपक्वतेसाठी स्थिर जोखीम-मुक्त व्याजदर आणि कोणतीही जोखीम मुक्त लवाद संधी नाहीत. या गृहितकांमुळे किमती वास्तविक परिणामांपासून विचलित होऊ शकतात.
- हे "ब्लॅक बॉक्स" मॉडेल आहे. याचा अर्थ असा की मॉडेल त्याच्या परिणामांवर कसे पोहोचते हे नेहमीच स्पष्ट नसते. यामुळे ऑप्शन्स किमतींवर परिणाम करणारे मूलभूत घटक समजून घेण्यासाठी मॉडेल वापरणे कठीण होऊ शकते.

